FUNCIÓN LINEAL

En geometría y el álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una línea recta. Esta función se puede escribir como:

donde m y b son constantes reales y x es una variable real. La constante m es la pendiente de la recta, y b es el punto de corte de la recta con el eje y. Si se modifica m entonces se modifica la inclinación de la recta, y si se modifica b, entonces la línea se desplazará hacia arriba o hacia abajo.

Algunos autores llaman función lineal a aquella con b= 0 de la forma:

mientras que llaman función afín a la que tiene la forma:

cuando b es distinto de cero.

EJEMPLOS

Una función lineal de una única variable dependiente x es de la forma:

que se conoce como ecuación de la recta en el plano x,y.

En la figura se ven dos rectas, que corresponden a las ecuaciones lineales siguientes:

en esta recta el parámetro m= 1/2 por tanto de pendiente 1/2, es decir, cuando aumentamos x en una unidad entonces y aumenta en 1/2 unidad, el valor de b es 2, luego la recta corta el eje y en el punto y= 2.

En la ecuación:

la pendiente de la recta es el parámetro m= -1, es decir, cuando el valor de x aumenta en una unidad, el valor de y disminuye en una unidad; el corte con el eje y es en y= 5, dado que el valor de b= 5.

En una recta el valor de m se corresponde al ángulo  de inclinación de la recta con el eje de las x a través de la expresión: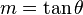

APLICACIONES EN LA VIDA COTIDIANA

Una de las realidades de la vida es la forma en que gran parte del mundo funciona mediante reglas matemáticas. Los sistemas lineales son una de las herramientas de las matemáticas que tienen múltiples usos en el mundo real. La vida está llena de situaciones en las que la salida de un sistema se duplica si la entrada se duplica y en donde la salida se corta a la mitad si la entrada hace lo mismo. Eso es lo que es un sistema lineal y cualquier sistema lineal puede describirse con una ecuación lineal.

Las funciones lineales, como hemos visto, sirven para describir multitud de fenó-

menos en los que se relacionan dos magnitudes que varían proporcionalmente.

Por ejemplo: volumen de un alimento 8 coste de este

 volumen de una cierta sustancia 8 peso de esta

 tiempo de movimiento uniforme 8 distancia recorrida

Todas ellas se representan mediante rectas sobre las cuales se aprecia cómo varía 

una magnitud respecto a la otra.

Problemas resueltos

1. 

Geometría 

es una rama de la matemática que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos, politopos (que incluyen paralelas,perpendiculares, curvas, superficies, polígonos, poliedros, etc.)

•  Aplicaciones De La Geometría
•  Es la base teórica de la geometría descriptiva o del dibujo técnico. - También da fundamento a instrumentos como el compás, el teodolito, el fotógrafo o el sistema de posicionamiento global.
•  Aplicaciones en la Astronomía:Tiene su aplicación práctica en física aplicada, mecánica,arquitectura, cartografía, astronomía, náutica, topografía, balística, etc. Y es útil en la preparación de diseños e incluso en la elaboración de artesanías.
• Aplicación en la Topografía :Los mapastopográficos utilizan el sistema de representación de planos acotados,mostrando la elevación del terreno utilizando líneas que conectan los puntos con la misma cota respecto de un plano de referencia,
• Geometría Descriptiva: La geometría descriptiva es un conjunto de técnicas de carácter geométrico que permite representar el espacio tridimensional sobre una superficie bidimensional. 
•  Axiomas, definiciones y teoremas:En geometría Euclidiana, los Axiomas y Postulados son proposiciones querelacionan conceptos, definidosen función del punto, la recta y el plano.
• 8. Otras Ramas de la Geometría- La Geometría Elíptica (geometría de Riemann)- La Geometría Hiperbólica de Nikolái Lobachevski.